4) Calcul de l’âge moyen trace de fission

II.1.4. Calcul de l’âge moyen trace de fission

La datation par traces de fission correspondant à un processus de désintégration nucléaire suit, comme d’autres méthodes isotopiques, la loi de décroissance radioactive. Le nombre d’isotopes "père" décroît selon une loi exponentielle avec le temps. Le taux de désintégration dN/dt d’un isotope est proportionnel au nombre d’atomes N présent à un temps t.

Le principe correspond à la loi de décroissance radioactive (1) avec néanmoins quelques adaptations (2).

Dans la méthode de datation par trace de fission, le nombre d’atome fils correspond au nombre de traces accumulées dans un cristal. Corrélativement, le nombre de traces latentes s’accumulant dans un cristal augmente au cours du temps.

La décroissance de l’²³⁸U ne se réalise pas par le seul processus de fission spontanée mais également par décroissance α. La constante de décroissance totale (λ) peut être approchée par la constante de décroissance α (λ_α). Ainsi, la correction du nombre de traces permettant de prendre en compte ce phénomène s’effectue à partir du rapport λ_f/ λ où λ_f correspond à la constante de fission. La valeur de λ peut être approchée avec λ_α avec λ = λ_f  + λ_α = λ_α avec λ_f  variant entre de 7,03 à 8,46.10^-17 an^-1 (Bigazzi, 1981). λ_f est inférieur d’un facteur 10⁶ par rapport à λ_α dont la valeur est égale à 1,55.10^-10 an^-1 (Steiger et Jäger, 1977).

La densité de traces ρ_s, correspondant au nombre de traces spontanées par cm² (déterminée sur surface interne du cristal polie et traitée chimiquement) est fonction du temps et de la teneur en ²³⁸U.

Etablir la densité de traces spontanées (ρ_s) n’est toutefois pas suffisante pour déterminer l’âge trace de fission d’un minéral. Un autre paramètre de concentration est nécessaire : celui de l’²³⁸U (élément père) ou un paramètre qui en dépend. Le rapport des abondances isotopiques ²³⁵U/²³⁸U est une constante connue. Il est donc possible de déterminer la teneur en ²³⁸U si l’on est capable de mesurer celle de l’²³⁵U.

La détermination de la concentration en ²³⁵U s’opère en provoquant sa fission induite, c'est-à-dire artificiellement grâce à un réacteur nucléaire. La fission induite des atomes d’²³⁵U est déclenchée par capture neutronique grâce à une irradiation générant un flux de neutrons thermiques faiblement énergétique (< à 0,2 MeV). Les échantillons ont été irradiés dans le canal P1 du réacteur ORPHEE au CEA de Saclay (Commissariat à l’Energie Atomique, laboratoire Pierre Süe). Les caractéristiques du canal P1 ont été décrites par Meyer (1990). La fluence demandée est de 4,9.10¹⁵ neutrons/cm² soit 6 minutes d’irradiation pour un flux nominal estimé de 1,37.10¹³ neutrons/cm²/s.

La densité de traces induites (ρ_i) ainsi générées dans un minéral irradié est dépendante de la concentration en ²³⁵U et de la fluence Φ utilisée. La constante de désintégration par fission spontanée de ²³⁸U (λ²³⁸U) étant supposée connue, ce système peut, dans ce cas, jouer le rôle de géochronomètre en tenant compte de la composition isotopique I = ²³⁵U/²³⁸U de l'uranium qui est constante dans l’actuel.

Le comptage est ainsi effectué sur deux types de support d’où l’introduction d’un facteur géométrique g. Le facteur g correspond au rapport entre la géométrie de type 4π stéradians pour une observation réalisée dans un volume cristallin (l’échantillon) et 2π stéradians pour une observation réalisée sur un détecteur externe. Sur ce dernier, l’observation s’effectue sur une surface (g = g_i/g_s) où g est une valeur purement théorique.

D’après Gleadow et Lovering (1977), le fait de travailler sur des cristaux d’apatite dont les faces sont parallèles à l’axe cristallographique c avec un détecteur externe en muscovite, permet d’obtenir la constance du paramètre g approchant la valeur de 0,5.

A partir de ces conditions, l’équation d’âge par traces de fission (3) peut se présenter sous cette forme,

La dosimétrie neutronique est assurée par des pastilles de verre (dosimètre), ou "moniteurs", contenant une concentration connue en uranium. Ces dosimètres sont irradiés conjointement aux cristaux à dater et sont utiles pour caractériser la fluence neutronique. Leur irradiation provoque la fission de l’²³⁵U par capture neutronique. La fluence est déterminée, après irradiation, par comptage des traces de fission induites produites dans le moniteur.

Les neutrons interagissent avec les échantillons  En effet, le flux entrant de neutrons sera différent du flux sortant et variable d’une session d’irradiation à une autre (Tab.2). La détermination de ce flux en différents points équidistants va être donnée par la densité moyenne des traces induites « imprimées » sur le détecteur externe des dosimètres (ρ_verre). Les densités moyennes de traces issues des trois dosimètres seront utilisées pour le calcul du facteur zêta décrit plus en aval.

Date d'irradiation	Mai 2003	Fév. 2004	Oct. 2005	Déc. 2005	Avril 2006	Mai 2007	Juin 2008	Juin 2008 (2)
% de variation max. entre 3 dosimètres	2,17	2,01	7,96	0,84	4,46	3,22	1,85	2,84

 Tab. 2: Pourcentages de fluctuation du flux neutronique à travers les montages comparés entre plusieurs séquences d’irradiations. Le flux est variable d’une séance d’irradiation à l’autre et selon le montage du conteneur.

Il apparaît que le flux de neutrons ne présente pas d’évolution régulière du haut vers le bas du conteneur. Il est donc possible que des variations intermédiaires entre deux dosimètres aient lieu. Les variations latérales du flux neutroniques sont plus importantes par rapport aux variations verticales (Fig. 20). Il existe un gradient pouvant être supérieur à l’écart existant entre les trois dosimètres (selon la position du dosimètre dans le conteneur).

La densité de traces induites, enregistrée par les détecteurs externes associés aux pastilles de verre (ρ_d), est proportionnelle à la fluence Φ, c'est-à-dire :

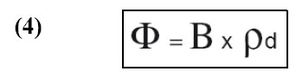
B est une constante caractéristique du dosimètre en relation avec le flux neutronique (facteur de proportionnalité). Il exprime le rapport entre les neutrons et les traces induites. En combinant les expressions (3) et (4), l’équation d’âge devient ainsi :

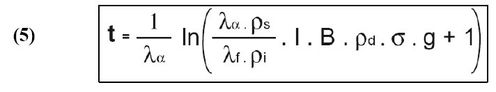
Néanmoins, l’équation d’âge sous cette forme pose problème. En effet, la détermination du paramètre B et donc la fluence neutronique Φ (4) est très délicate à obtenir et réclame une expérimentation lourde (De Corte et al., 1991 ; Van den Haute et al., 1988). La valeur du λ_f n’est connue qu’à environ 15 %. L’utilisation d’une forme différente de l’équation d’âge et l’introduction d’un nouveau paramètre de substitution zêta (ζ) permettent de contourner cette complication (6).

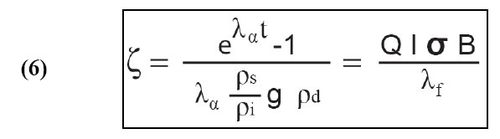
La méthode du zêta (Hurford et Green, 1983) permet d’intégrer les termes difficiles à déterminer dans un seul facteur.  ζ est un paramètre déterminé de manière expérimentale par calibration à partir de standards (échantillons d’âge connu). La valeur ζ doit être déterminée par chaque observateur (Hurford, 1990). Cette valeur dépend des conditions de révélation et d'observation des traces (façon de compter les traces de fission au microscope représentée par le paramètre Q : facteur d’observation). ζ varie également selon le verre moniteur utilisé (dosimètre) et les laboratoires (thermalisation des neutrons du réacteur, position d’irradiation).

La détermination expérimentale du facteur ζ est réalisée à partir de plusieurs échantillons de cristaux d’apatite reconnus internationalement en terme de standard et dont l’âge est parfaitement connue par le biais de plusieurs méthodes de datation absolue (K/Ar et ⁴⁰Ar/³⁹Ar). La détermination du facteur ζ est réalisée conformément aux recommandations de l’I.U.G.S. (Hurford, 1990) spécifiant au minimum l’utilisation de trois irradiations et deux standards pour obtenir un facteur z moyen valide.

Deux apatites ont été sélectionnées comme standard d’âge par la sous-commission de géochronologie de l’I.U.G.S. (Hurford, 1990) :

-         Durango (31,40 ± 0,72 Ma : Naeser et Fleischer, 1975 ; Farley et al., 1996) ;

-         Fish Canyon (27,74 ± 0,72 Ma : Stevens et al., 1967 ; Hurford et Hammerschmidt, 1985 ; Kunk et al., 1985).  

Dans nos mesures, les standards de Durango et de Fish Canyon Tuff ont été utilisés pour la détermination du facteur de calibration Zeta (z) appliqué aux cristaux d’apatite.

Le facteur z moyen est obtenu à partir de la moyenne pondérée (7) des différentes valeurs de z  individuels (ZMPS : Zêta Moyen Pondéré Standard ; Green, 1985). L’inverse de l’erreur sur chaque valeur (±1σ) correspond au facteur de pondération.

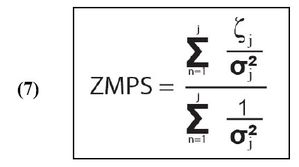
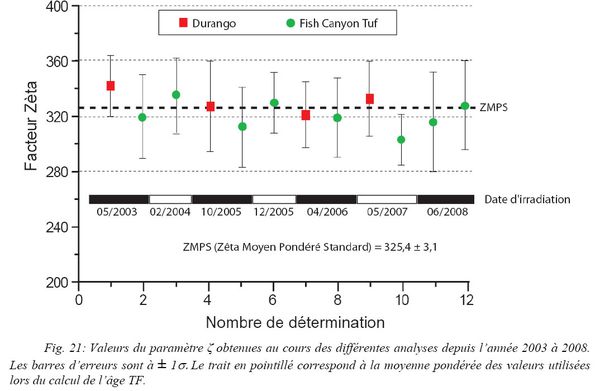
Douze échantillons étalons provenant de huit irradiations différentes avec leurs dosimètres associés ont été mesurés pour déterminer le facteur z  personnel (Tab. 3 ; Fig. 21). 

La valeur pondérée personnelle du z  est de 325 ± 3 (avec l’emploi de dosimètres CN5). Les valeurs du z  fluctuent faiblement au cours des mesures dans le temps et des multiples irradiations (Fig. 21). Cette valeur pondérée a été adoptée pour l’ensemble des datations présentées dans ce travail.

L’expression finale de l’équation d’âge utilisée dans ce travail, selon la méthode du détecteur externe, s’écrit telle que :

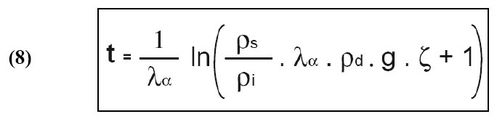
La méthode de l'âge central (Galbraith et Laslett, 1993) a été utilisée pour le calcul de l'âge TF de chaque échantillon. Cette méthode permet de calculer la moyenne de la distribution logarithmique des âges individuels correspondant aux âges des différents grains analysés. Elle permet également de reconnaître la variation des âges et l’existence de plusieurs populations de grains.